Spigot algorithms for the digits of pi in Python

Introduction

If you ever had to work on a Python project that required the computation of a large number of π’s digits and wanted to generate them on the spot instead of downloading them from the web, you might have stumbled upon a series of innocent looking functions based on so-called Spigot Algorithms. A Spigot Algorithm is an algorithm meant to produce digits of a transcendental number sequentially from left to right while maintaining a low profile in terms of memory usage, something very important for older computing devices.

The Rabinowitz-Wagon algorithm

One of the first known algorithms of this type comes from A. Sale who, in 1968, devised a method to evaluate the digits of e[1]. Twenty years later, D. Saada proposed the use of a similar algorithm for the computation of π and in 1991 so did math hacker Stanley Rabinowitz.

The latter further explored the concept in 1995 with his colleague Stan Wagon in an article in The American Mathematical Monthly[2]. In 2004 Jeremy Gibbons addressed one of the biggest weaknesses of the Rabinowitz-Wagon algorithm—the fact that the computation is bounded by design (meaning that one has to commit in advance to compute a certain number of digits)—in a separate American Mathematical Monthly article[3]. His proposed solution took advantage of the concept of streaming algorithms, something that allowed the calculation to run indefinitely.

Rabinowitz and Wagon’s algorithm was based on the following expression derived from the Leibniz formula for π:

$$\pi = 2 + {1 \over 3} \left(2 + {2 \over 5} \left(2 + {3 \over 7} \left(\cdots\left(2 + {i \over 2i + 1}\bigg(\cdots\bigg)\right)\right)\right)\right) \tag1$$

One implementation of such an algorithm comes from Dik T. Winter, Achim Flammenkamp and others[4] in the form of the following tiny ANSI C program which calculates 15000 decimal places of π:

a[52514],b,c=52514,d,e,f=1e4,g,h;main(){for(;b=c-=14;h=printf("%04d",e+d/f))for(e=d%=f;g=--b*2;d/=g)d=d*b+f*(h?a[b]:f/5),a[b]=d%--g;}

Gibbons later used the same expression to create his first streaming algorithm for the digits of π. A slightly altered version of his Haskell implementation is showcased below.

import Data.Ratio

type LFT = (Integer, Integer, Integer, Integer)

extr :: LFT -> Integer -> Rational
extr (q,r,s,t) x = (q * x + r)%(s * x + t)

-- apply stream to create an infinite list of output terms, each of type c.
stream :: (b->c) -> (b->c->Bool) -> (b->c->b) -> (b->a->b) -> b -> [a] -> [c]
stream next safe prod cons z (x:xs)
  = if    safe z y
    then y : stream next safe prod cons (prod z y) (x:xs)
    else stream next safe prod cons (cons z x) xs
      where y = next z

-- when a transformation is represented by its four coefficients q,r,s and t 
-- arranged as a matrix, function composition corresponds to matrix multiplication.
comp :: LFT -> LFT -> LFT
comp (q,r,s,t) (u,v,w,x) = (q*u+r*w,q*v+r*x,s*u+t*w,s*v+t*x)

-- generate pi based on the Leibniz series for pi
leibniz_pi = stream next safe prod cons init lfts where
    init      = (1,0,0,1)
    lfts      = [(k, 4*k+2, 0, 2*k+1) | k<-[1..]]
    next z    = floor (extr z 3)
    safe z n  = (n == floor (extr z 4))
    prod z n  = comp (10, -10*n, 0, 1) z
    cons z z' = comp z z'

main = print (take 10 leibniz_pi)

$ ./main
[3,1,4,1,5,9,2,6,5,3]

If you’d like to tinker around with the code, I’ve uploaded it to Replit where you can also test it out for a larger number of digits.

Through various optimizations he then condensed the code into the following much smaller, but rather obscure, Haskell program.

leibniz_pi = g(1,0,1,1,3,3) where
   g(q,r,t,k,n,l) = if 4*q+r-t<n*t
     then n : g(10*q,10*(r-n*t),t,k,div(10*(3*q+r))t-10*n,l)
     else g(q*k,(2*q+r)*l,t*l,k+1,div(q*(7*k+2)+r*l)(t*l),l+2)
main = print (take 10 leibniz_pi)

By translating this code, we get one of the most common Python functions for the generation of π found across the web:

# From https://mail.python.org/pipermail/edu-sig/2006-July/006810.html
# John Zelle 4-5-06
# (edited for Python 3)
def leibniz_pi():
    """generator for digits of pi"""
    q,r,t,k,n,l = 1,0,1,1,3,3
    while True:
        if 4*q+r-t < n*t:
            yield n
            q,r,t,k,n,l = (10*q,10*(r-n*t),t,k,(10*(3*q+r))//t-10*n,l)
        else:
            q,r,t,k,n,l = (q*k,(2*q+r)*l,t*l,k+1,(q*(7*k+2)+r*l)//(t*l),l+2)

pi = leibniz_pi()
print([next(pi) for _ in range(10)])

$ python3 digits.py
[3, 1, 4, 1, 5, 9, 2, 6, 5, 3]

Notice the use of the yield keyword which makes the function behave like an iterator. This generator function pattern is what allows us to iterate through as many digits as we might need without having to keep them all in memory or calculate them beforehand.

If you’d like to learn more about how Gibbons’ spigot algorithm uses expression (1) and the concept of streaming algorithms to produce the digits of π, the original paper does a great job at explaining the entire process while also going through some of the basics of lazy functional programming in Haskell.

Using Lambert’s expression

In the final pages of his 2004 paper, Gibbons presents two more spigot algorithms for the digits of π based on different expressions that are more efficient than the one originally used by Rabinowitz and Wagon. The first one is known as Lambert’s expression:

$$\pi = {4 \over 1 + {1^2 \over 3 + {2^2 \over 5 + {3^2 \over 7 + \cdots}}}} \tag2$$

from which the following Haskell program can be derived:

import Data.Ratio

type LFT = (Integer, Integer, Integer, Integer)

-- apply stream to create an infinite list of output terms, each of type c.
stream :: (b->c) -> (b->c->Bool) -> (b->c->b) -> (b->a->b) -> b -> [a] -> [c]
stream next safe prod cons z (x:xs)
  = if    safe z y
    then y : stream next safe prod cons (prod z y) (x:xs)
    else stream next safe prod cons (cons z x) xs
      where y = next z

-- when a transformation is represented by its four coefficients q,r,s and t 
-- arranged as a matrix, function composition corresponds to matrix multiplication.
comp :: LFT -> LFT -> LFT
comp (q,r,s,t) (u,v,w,x) = (q*u+r*w,q*v+r*x,s*u+t*w,s*v+t*x)

-- generate pi based on Lambert's expression 
lamberts_pi = stream next safe prod cons init lfts where
  init                 = ((0,4,1,0), 1)
  lfts                 = [(2*i-1, i*i, 1, 0) | i<-[1..]]
  next ((q,r,s,t),i)   = floor ((q*x+r) % (s*x+t)) where x = 2*i-1
  safe ((q,r,s,t),i) n = (n == floor ((q*x+2*r) % (s*x+2*t)))
        where x=5*i-2
  prod (z,i) n         = (comp (10, -10*n, 0, 1) z, i)
  cons (z,i) z'        = (comp z z', i+1)
  
main = print (take 10 lamberts_pi)

$ ./main
[3,1,4,1,5,9,2,6,5,3]

You can try out this version of the code here.

After condensing the code like before, what I got was the following:
(I’d love to hear about any further optimizations you might come up with.)

lamberts_pi= g(0,4,1,0,4,1) where
   g(q,r,s,t,n,i) = if n == div(q*(5*i-2)+2*r)(s*(5*i-2)+2*t)
     then n : g(10*q-10*n*s, 10*r-10*n*t,s,t,div(10*((q-n*s)*(2*i-1)+r-n*t))(s*(2*i-1) + t), i)
     else g((2*i-1)*q+r, i*i*q, (2*i-1)*s + t, i*i*s, div((5*i*i-1)*q + (2*i+1)*r)((5*i*i-1)*s+(2*i+1)*t),i+1)
main = print (take 10 lamberts_pi)

and by translating to Python:

def gibbons_lamberts_pi():
    q,r,s,t,n,i = 0,4,1,0,4,1
    while True:
        if n == (q*(5*i-2)+2*r)//(s*(5*i-2)+2*t):
	    yield n
	    q,r,s,t,n,i = 10*q-10*n*s,10*r-10*n*t,s,t,(10*((q-n*s)*(2*i-1)+r-n*t))//(s*(2*i-1)+t),i
        else:
	    q,r,s,t,n,i = (2*i-1)*q+r,i*i*q,(2*i-1)*s+t,i*i*s,((5*i*i-1)*q+(2*i+1)*r)//((5*i*i-1)*s+(2*i+1)*t),i+1
pi = gibbons_lamberts_pi()
print([next(pi) for _ in range(10)])

$ python3 lamberts.py
[3, 1, 4, 1, 5, 9, 2, 6, 5, 3]

This program is about five times faster than the one using expression (1) although we can still do better. The following Python function which is also very popular and based on Lambert’s expression, is actually quite faster than the one proposed by Gibbons.

# Found here: https://gist.github.com/deeplook/4947835#file-pi_digits-py
# Modified to become unbounded.
def lamberts_pi():
    k, a, b, a1, b1 = 2, 4, 1, 12, 4
    while True:
        p, q, k = k * k, 2 * k + 1, k + 1
        a, b, a1, b1 = a1, b1, p * a + q * a1, p * b + q * b1
        d, d1 = a / b, a1 / b1
        while d == d1:
            yield int(d)
            a, a1 = 10 * (a % b), 10 * (a1 % b1)
            d, d1 = a / b, a1 / b1
pi = lamberts_pi()
print([next(pi) for _ in range(10)])

$ python3 pi_digits.py
[3, 1, 4, 1, 5, 9, 2, 6, 5, 3]

This algorithm appears as an example for the power of the ABC programming language and its unbounded numbers in a book called The ABC Programmer’s Handbook, originally published in 1990 (see here).

HOW TO PI:
    PUT 2, 4, 1, 12, 4 IN k, a, b, a', b'
    WHILE 1=1:
        NEXT APPROXIMATION
        PRINT COMMON DIGITS
NEXT APPROXIMATION:
    PUT k**2, 2*k+1, k+1 IN p, q, k
    PUT a', b', p*a+q*a', p*b+q*b' IN a, b, a', b'
PRINT COMMON DIGITS:
    PUT floor(a/b), floor(a'/b') IN d, d'
    WHILE d = d':
        WRITE d<<1
        PUT 10*(a mod b), 10*(a' mod b') IN a, a'
        PUT floor(a/b), floor(a'/b') IN d, d'

It also appears as an example within the official Ruby repository since 1998 (see here).

#!/usr/local/bin/ruby

k, a, b, a1, b1 = 2, 4, 1, 12, 4
loop do
  # Next approximation
  p, q, k = k*k, 2*k+1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  # Print common digits
  d = a / b
  d1 = a1 / b1
  while d == d1
    print d
    $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end

Obviously the Python implementation shown above is just a direct translation of these programs. A summary of how this algorithm works is provided by the authors of The ABC Programmer’s Handbook:

The program works by repeatedly refining a so-called continued fraction that represents pi. The first approximation is \(4 \over 1\), the second is \(4 \over {1 + {1 \over 3}}\), which is \(12 \over 4\). In the next, the 3 is replaced by \(3 + {4 \over 5}\), and in the next after that, the 5 is replaced by \(5 + {9 \over 7}\) and so on, so that each part of the fraction is \(k^2 \over {2k+1+…}\) for \(k = 0, 1, 2, …\)

In the program, a/b represents one approximation of the fraction, and a’/b’ the next. If there are any leading digits in common, then these are printed, and the next approximation is calculated.

This is by far the fastest algorithm I’ve found that’s based on Lambert’s expression.

Using Gosper’s series

Gibbons concludes his paper by introducing an algorithm based on an even more efficient expression for π attributed to Bill Gosper:

$$\small{\pi = 3 + {1 \times 1 \over 3 \times 4 \times 5} \times \left( 8 + {2 \times 3 \over 3 \times 7 \times 8} \times \left( \cdots 5i-2 + {i(2i-1) \over 3(3i+1)(3i+2)} \times \cdots \right) \right)\tag3}$$

The complete Haskell program derived from this series is the following:

import Data.Ratio

type LFT = (Integer, Integer, Integer, Integer)

-- apply stream to create an infinite list of output terms, each of type c.
stream :: (b->c) -> (b->c->Bool) -> (b->c->b) -> (b->a->b) -> b -> [a] -> [c]
stream next safe prod cons z (x:xs)
  = if    safe z y
    then y : stream next safe prod cons (prod z y) (x:xs)
    else stream next safe prod cons (cons z x) xs
      where y = next z

-- when a transformation is represented by its four coefficients q,r,s and t arranged as a matrix, function composition corresponds to matrix multiplication.
comp :: LFT -> LFT -> LFT
comp (q,r,s,t) (u,v,w,x) = (q*u+r*w,q*v+r*x,s*u+t*w,s*v+t*x)

-- generate pi based on Gospers's series 
gospers_pi = stream next safe prod cons init lfts where
  init                 = ((1,0,0,1), 1)
  lfts                 = [let j = 3*(3*i+1)*(3*i+2)
                          in (i*(2*i-1),j*(5*i-2),0,j) | i<-[1..]]
  next ((q,r,s,t),i)   = div (q*x+5*r) (s*x+5*t) where x = 27*i-12
  safe ((q,r,s,t),i) n = (n == div (q*x+125*r) (s*x+125*t))
                         where x=675*i-216
  prod (z,i) n         = (comp (10, -10*n, 0, 1) z, i)
  cons (z,i) z'        = (comp z z', i+1)
  
main = print (take 10 gospers_pi)

$ ./main
[3,1,4,1,5,9,2,6,5,3]

You can try out this version of the code here.

By condensing the program like before and converting it to Python, what we get is the following:

def gospers_pi():
    q,r,t,n,i = 1,0,1,8,1
    while True:
        if n == (q*(675*i-216)+125*r)//(125*t):
            yield n
            q,r = 10*q,10*r-10*n*t
        else:
            q,r,t,i = i*(2*i-1)*q,3*(3*i+1)*(3*i+2)*((5*i-2)*q+r),3*(3*i+1)*(3*i+2)*t,i+1
        n = (q*(27*i-12)+5*r) // (5*t)
pi = gospers_pi()
print([next(pi) for _ in range(10)])

$ python3 gospers.py
[3, 1, 4, 1, 5, 9, 2, 6, 5, 3]

This function performs slightly better than the one Gibbons proposed based on Lamberts expression.

The open problem

Jeremy Gibbons concludes his paper by making a conjecture that, if proven, would substantially improve his spigot algorithm based on Gosper’s series. The conjecture is the following:

Define the following functions: $$ \begin{align} n(z,i) &= \left\lfloor {z\left(\tfrac{27i + 15} {5}\right)} \right\rfloor\\ p((z,i),n) &= (z\big(\begin{smallmatrix} 10 & -10n\\0 & 1\end{smallmatrix}\big), i) \\ c((z,i),z') &= (zz',i+1)\\ s((z,i),n) &= (n = \left\lfloor {z\left(\tfrac{675i - 216} {125}\right)} \right\rfloor)\\ \end{align} $$ For \(i = 1,2\dots\), let $$ \begin{align} x_i &= \big(\begin{smallmatrix} i(2i-1) & 3(3i+1)(3i+2)(5i-2)\\0 & 3(3i+1)(3i+2)\end{smallmatrix}\big)\\ u_0 &= (\big(\begin{smallmatrix}1 & 0\\0 & 1\end{smallmatrix}\big), 1)\\ u_i &= p(v_i, y_i)\\ v_i &= c(u_{i-1}, x_i)\\ y_i &= n(v_i)\\ \end{align} $$ Then \(s(v_i,y_i)\) holds for all \(i\).

If the conjecture holds, the Haskell program becomes:

piG3 = g(1,180,60,2) where
  g(q,r,t,i) = let (u,y)=(3*(3*i+1)*(3*i+2),div(q*(27*i-12)+5*r)(5*t))
               in y : g(10*q*i*(2*i-1),10*u*(q*(5*i-2)+r-y*t),t*u,i+1)
main = print (take 10 piG3)

$ ./main
[3,1,4,1,5,9,2,6,5,3]

Or, translated into Python:

def gospers_pi_unproven():
    q,r,t,i = 1, 180, 60, 2
    while True:
        u,y = 3*(3*i+1)*(3*i+2), (q*(27*i-12)+5*r)//(5*t)
        yield y
        q,r,t,i = 10*q*i*(2*i-1),10*u*(q*(5*i-2)+r-y*t),t*u,i+1
pi = gospers_pi_unproven()
print([next(pi) for _ in range(10)])

$ python3 piG3.py
[3, 1, 4, 1, 5, 9, 2, 6, 5, 3]

This version of the program is considerably faster than all other spigot type algorithms I’ve tested. Of course, because the conjecture is still unproven, this algorithm is not guaranteed to produce the correct digits for π indefinitely (although I did in fact test it successfully up to one million digits).

Side by side comparison and summary

Even though spigot algorithms are not that useful today, it is very nice seeing how they perform on modern hardware. Below is a graph showcasing the difference in speed between the various algorithms introduced throughout this article.

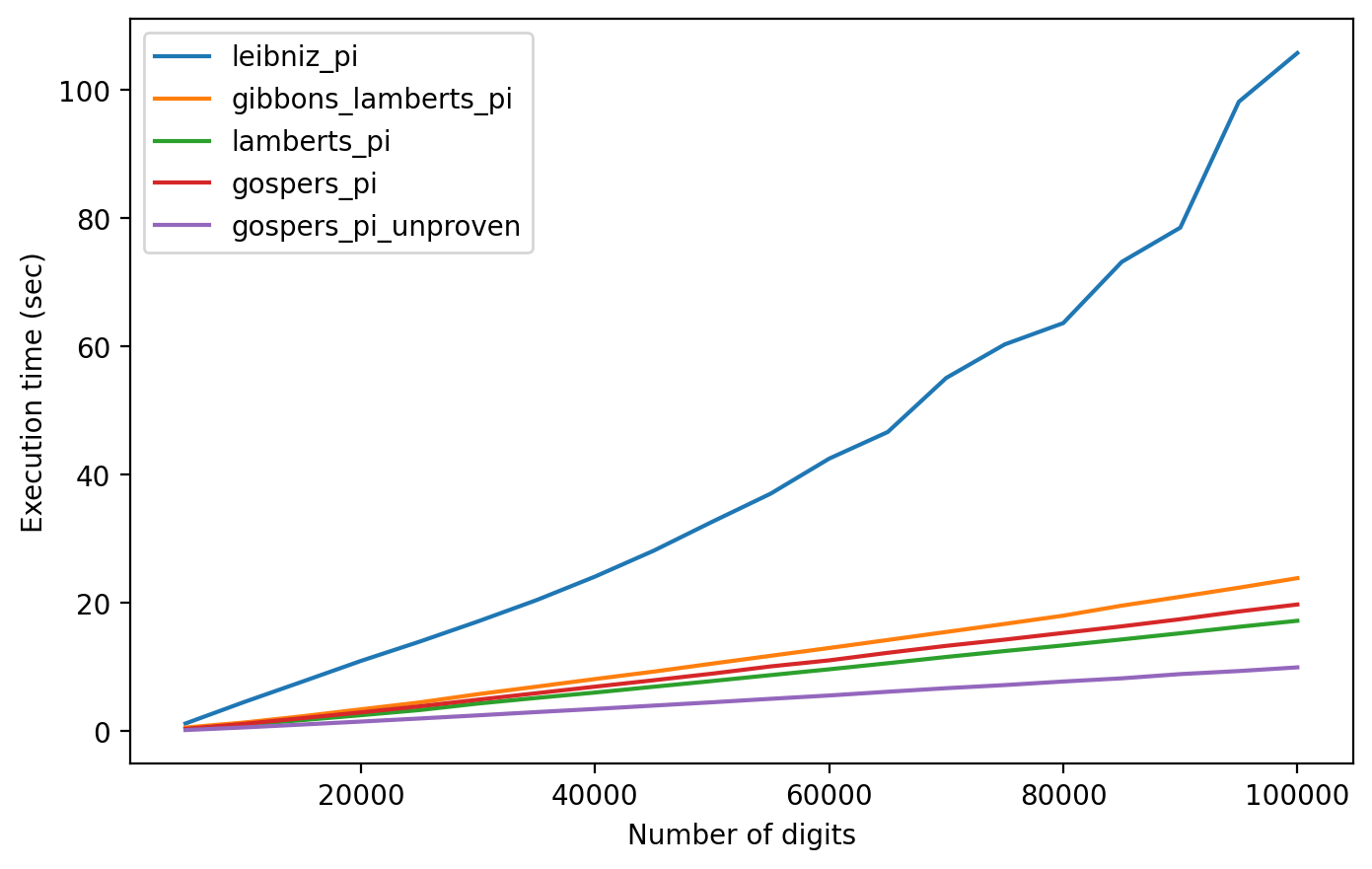A side by side comparison of different spigot algorithms

If you'd like to learn more about how I tested and timed the various algorithms you can see some of the code I used by clicking here.

You can see how the algorithm derived from the Leibniz series, originally proposed by Rabinowitz and Wagon and later improved by Gibbons is extremely slow compared to the others. On the other end of the spectrum, the algorithm produced using Gosper’s expression is about 10 times faster, although still based on an unproven conjecture.

Even though there is probably no reason for you to generate a large number of π’s digits by yourself, especially using slow spigot algorithms, I hope you found this small glimpse into the past of computing as interesting as I did. If you have any suggestions or comments, please feel free to contact me using any method of communication listed on the sidebar of this page.

---

References

1. A. H. J. Sale, “The Calculation of e to Many Significant Digits,” The Computer Journal, vol. 11, no. 2, pp. 229–230, Aug. 1968, doi: 10.1093/comjnl/11.2.229. [Online]. Available: https://academic.oup.com/comjnl/article-lookup/doi/10.1093/comjnl/11.2.229
2. S. Rabinowitz and S. Wagon, “A Spigot Algorithm for the Digits of Pi,” The American Mathematical Monthly, vol. 102, no. 3, pp. 195–203, Mar. 1995, doi: 10.1080/00029890.1995.11990560. [Online]. Available: https://www.tandfonline.com/doi/full/10.1080/00029890.1995.11990560
3. J. Gibbons, “Unbounded Spigot Algorithms for the Digits of Pi,” The American Mathematical Monthly, vol. 113, no. 4, pp. 318–328, Apr. 2006, doi: 10.1080/00029890.2006.11920310. [Online]. Available: https://www.tandfonline.com/doi/full/10.1080/00029890.2006.11920310
4. J. Arndt and C. Haenel, Pi - Unleashed. Springer Science & Business Media, 2001.